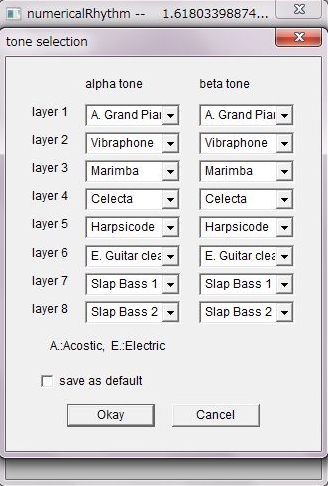
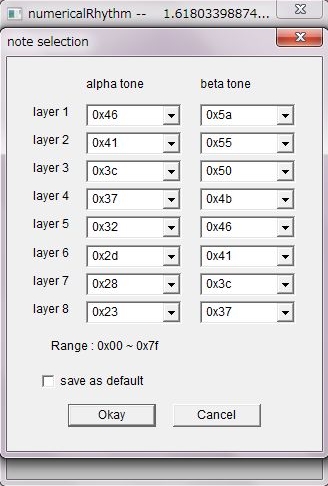
音楽のリズムは、2ビート，3ビート，4ビート，8ビート等と、単純な構造の繰り返しを意味します。
楽譜では、拍子(beat time)として、1拍(beat)の音符(note)の長さと1小節(bar)あたりの拍数(count of beats)を最初に記します。この拍子は実際的な組み合わせとして、複合拍子(compound time)や混合拍子(odd meter)を含め、約20通り余り(？)出来ますが、リズムとしての基本構造は、2ビート，3ビート，4ビートの単純拍子(simple time)となります
例えば、6/8 timeは2ビートです。1拍の中に8分音符が3つある2ビートです

準結晶構造のリズムは、様々な言い方が出来ます、――
2ビートと3ビートの複合リズムと言えればいいのですが、音楽で言う複合拍子の様に単純なユニットを繰り返す訳ではありません。
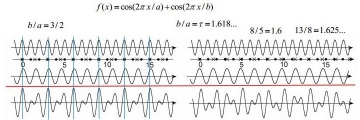
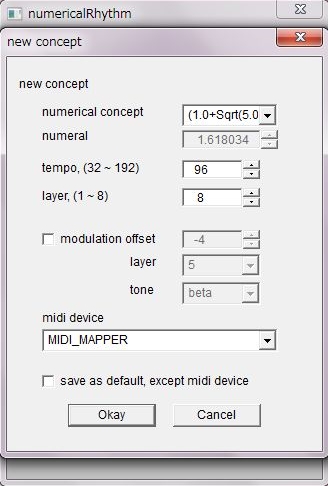
f(x) = cos(2 * PI * x) + cos(2 * PI * x / r) とすれば(一次元)準結晶構造の(リズム)周期を示す事になります。但し r は黄金比で、r = (1 + Sqr(5)) / 2
(三次元)物質の原子配列に倣えば、準結晶は(長距離)秩序があります。アモルファスにはありませんが結晶にもあります。秩序があるという点で両者は同様です。数学的には、音楽で使われているリズムは結晶構造です。では、準結晶構造のリズムはどの様なものでしょうか。
この比較の良いメタファーと思われる対比が植物の進化にみられます


ゲーテプランツェンと言われる植物があります(左画像)。これは俗称で、ゲーテが研究していた植物だからそう言われているだけで、ベンケイソウという名のとても原始的な植物です。ゲーテが研究していた株の子孫を、ゲーテの孫から貰った人がいて、わたしもその御裾分けに預かりました。実際に育ててみると、その形態や繁殖方法の原始的で粗野なビヘイビアーに驚かされます。わたし達が、例えば花屋さんで、よく見かける多くの植物はずっと洗練されています

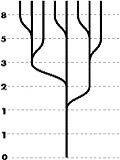
どの様な植物か概要を記すと、葉のキョシに自らのコピ−を生み出します。つまり単性で自己増殖する訳です。全ての茎が幹から水平に一定の十字方向のみに張り出し、上から見ると葉が重なって見えます。とてもお莫迦な植物です。この構造を支配する法的(?)オペレータ(modulus operator)は「2」です

多くの(進化した)現代植物は、より複雑な形態を有しています。茎は幹を廻る対数螺旋上はフィボナッチ数列比のポイントから張り出します(右図)。つまり黄金比です。上から見ると，否どこから見ても，葉はカオティックに分散して見えます。お利口な植物たちです。準結晶構造(quasi-crystalline structure)をしている訳です

ポイントを列記すると、
全て黄金比を採用した植物の方が有利な構造なのです

植物も進化と共に採用するオペレーターとしての「数」が単純なものでは無くなっているのです。そして、現代的に採用されているのが黄金比なのです



準結晶構造は、1982年にダニエル・シェヒトマン(Daniel Shechtman)によって、AL-Mnの電子線回析により発見され、シェヒトマンは2011年のノーベル化学賞を授賞しています。左図は、Al-Pd-Mn合金の準結晶原子配列

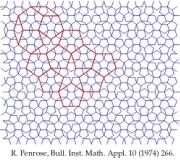
数学的には、1974年にロジャー・ペンローズ(Roger Penrose)の考案による二次元準周期構造(Penrose Tiling)があり、12〜13世紀のレオナルド・フィボナッチ(Leonardo Filius Bonacci)によるフィボナッチ数列は一次元準周期構造です

右図はふたつ共にペンローズタイリング

特徴を記す為の通例となる比較対象は結晶とアモルファスです。原子配列形態で比較する訳です。結晶及び準結晶は(長距離)秩序があり、アモルファスにはありません。
結晶と準結晶は、回転対称性が異なり、結晶は2,3,4,6回(180,120,90,60度数)の対称性があり、準結晶は5回対称性のみで、黄金比に満ちた構造になっています

準結晶を幾何学的に分類すると、三次元準結晶は、正二十面体準結晶のみです。二次元準結晶には、正十角形準結晶，正八角形準結晶，正十二角形準結晶などがあります

余談ですが、Stephen CollinsによるBob - Penrose Tiling Generator and Explorerというペンローズタイリングを描けるWindowsアプリケーションはとても面白いです



f(x) = cos(2 * PI * x) + cos(2 * PI * x / r) によって一次元準結晶構造のリズム周期を示せると記しました。但し r は黄金比で、r = (1 + Sqr(5)) / 2

この r を2や3にすると一次元結晶構造を示す事が出来ます。そしてそれはそのまま音楽のリズムとしての2拍子と3拍子になります。実際的な音だしには、ふたつの異なる音長乃至音調を組み合わせて表現します。三角関数を使う必要は無く、二次元格子を使って簡単に計算する事が出来ます。
また、r に無理数を使う事で、音楽には採用されていない奇妙なリズムを発声させる事が出来ます

これがこのソフトウエアの根幹となる機能です

先ず、Conceptを設定しなければPlay出来ません。
と言っても、唯単に数値を選択もしくは入力するだけの事です。デフォルトは黄金比です。他に、1.5，2，3，√2，√3，√5，e(自然数)，PI(π)の8つの数値がプリセットされており、「--input--」を選択する事で実数の入力が可能になります

Tempoを変化させる事が出来ます。大きな数値ほどテンポが速くなります

Layerは多層構造にする場合の層数です。
2つの音でリズム構造を表現する場合に、結晶構造であれ準結晶構造であれ、各々の音をその構造に従って細分化する事が出来ます。そうして全体の構造を歪める事もありません。というのも自己相似形をしているからです。
Layer1が最下位レベルで音構造としてはベースラインになります。(ナンバリングの大きな)上位のLayerは、下位のLayerを包含するより大きな構造となります。
Layerについては後述します

Modulationは音楽用語で言うところのmodulationではありません。実験的に導入してみただけの機能で、指定のLayerと音，その音に含まれる下位Layerの全ての音のキーを指定の数だけ変化(offset)させます。
numerical conceptとしての数値によって、指定のLayerと音の発声頻度が大きく変化する事に留意して下さい。試してみる事でよくわかると思います。
Modulationについては後述します

MIDI Deviceを設定する事が出来ます。
OSやサウンドデバイスに添付のソフトシンセだけでなく、Windowsが認識している外部MIDI機器の選択も可能です

MIDI Device以外の諸設定はデフォルトとしてセーブする事が出来ます


ver.0.95.00より、プリセットに2つの数値を追加しています。右の画像にはありませんが、(2 + Sqrt(8)) / 2 と (3 + Sqrt(13)) / 2 の2つで、黄金比同様に準結晶構造を創発するコンセプト数値です




Playボタン(乃至メニューのPlay)をクリックするだけです。恒久的にリズムを発声し続けます



Tone, Note, Velocityについて設定出来ます。各々、alpha toneとbeta toneの8つのLayerの計16の音について設定出来ます

これらの設定はGeneral MIDI規格そのものです。
16の音とは16チャンネルを使用するという事です。Toneについては楽器名から、Note, Velocityについては16進数の数値から選択します。MIDIに慣れていればわかり易いでしょう。一般的に10進数にした方が良かったかも知れませんが

設定値はデフォルトとしてセーブする事も出来ます。また、設定ファイルとしてセーブ，レストアする事も出来ます



もちろん、Conceptで設定したLayer数を越える音は無視されます





MIDI Setupファイルは好きなフォルダにセーブ，レストアする事が出来ます。サンプルファイルを、インストールフォルダの下位フォルダ「data」に収めてあります。お試し用です

右図はペンローズタイリングで、自己相似性がある事を示すもの。この特性は次元数が変わっても同じである。また、あまりにも明白過ぎる事だが、結晶構造にも同じ事が言える

一次元のリズムについてフィボナッチ数の生成法を使ってみる。高次LayerにA乃至Bの音があり、ルールとして、AにはABAを、BにはABを適用して、それを下位のLayerとする。これを繰り返して、第8Layerから第1Layerまで生成する。
――実際のプログラムでは、二次元格子により基調となるLayerを生成しながら、上位のLayerを順次生成していく

こうして生成される各Layerは各々全く同じ構造のものになる。もちろん相対的な次元距離は構造に従って異なる。このプログラムでは発声のタイミング(時間軸での距離)が異なるのだが、構造的には全てのLayerが同定的に発声する。
例えば、Aという一つの音の発声に割り振られた時間軸上で下位LayerではABAという3つの音が発声される。但し、下位Layerの一部を切り取ってその上位Layerを知る事は出来ない

Layer 1	ABAABABAABAABABAABABA	ABAABABAABAAB	ABAABABAABAABABAABABA	ABAABABAABAABABAABABA	ABAABABAABAAB
Layer 2	ABAABABA	ABAAB	ABAABABA	ABAABABA	ABAAB
Layer 3	ABA	AB	ABA	ABA	AB
Layer 4	A	B	A	A	B
Layer 5	A			B
Layer 6	A
Layer 7	A
Layer 8	A

1〜8でLayer数を設定する。1を設定すると基調となるLayerのみを発声する

黄金比をconceptにした場合、上記のテーブルから推察出来る様に、6，7，8を設定してもそれらの上位Layerの発声は稀になる。但し、それはnumerical concept次第であり、より大きな実数をconceptとして設定すると、上位Layerの発声頻度は高くなる。
――この辺りは展開を確認するか実際に発声させてみて確認出来る

実験的に導入してみただけの機能です。音楽用語で言うところのmodulationではありません



キーを変えます。noteの設定と同様にMIDI規格に準じ、数値で指定します



Layerを指定します。そのLayerの指定した音(alfa/beta)とそれに含まれる下位のLayer全ての音のキーを変える事になります。上位Layerには影響を与えません



alfa, betaのいずれかを選択します。指定したLayerでの選択された音とそれに含まれる下位Layerの音のキーが変わります