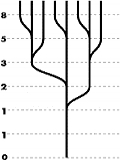
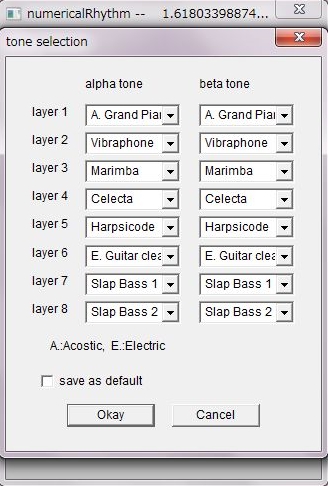
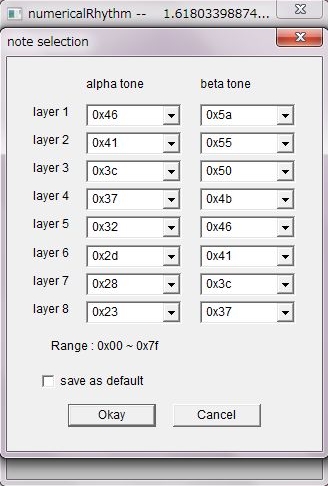
Two beats, three beats, four beats, eight beats and so on mean iteration of simple structural units.
In a musical score, a note of a beat and count of beats of a bar are wrote at first, as a beat time. This beat time could be around twenty schemes including compound time and odd meter though, basic structure as the rhythm are simple beats as two beats and three beats, four beats.
For an example, 6/8 time is a two beats, in which one beat has three eighth notes.
Quasicrystal rhythm could be in various phrase. --
It would be simple if the quasicrystal rhythm was a compound of two beats and three beats, it's not iteration of simple structural unitss.
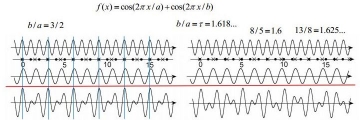
f(x) = cos(2 * PI * x) + cos(2 * PI * x / r) -- this formula is a complete expression of the one dimentional quasicrystal structural rhythm. r is the Golden Mean -- r = (1 + Sqr(5)) / 2
After the model of three dimentional atomic arrangement, crystal structure and quasicrystal structure form an orderly pattern, but amorphous does not. In that regard crystal structure and quasicrystal structure are same. In mathematically, musical rhythms are crystal structures. And then how is the quasicrystal structural rhythm?
There is a good metaphor of these comparison in the evolution of the plant.
Here is the Goethe Pflanzen(left picture) which is a vernacular term in Germany because Johann Wolfgang von Goethe researched the plant. It's named Brutblatt which is very primitive plant. A man received offspring of the plant researched by Goethe from Goethe's grandchild, and I got the share. I've cultivated it as a practical matter and I'd surprised at its behaviors which morphology and propagation method are very boorish and primitive. Modern plants are more accomplished, e.g. plants in a flower shop.
About characteristics it creates self-copy at edge of a leaf, i.e. it's monogenetic. All caulomes throw out in same cross shape, and when viewed from above leaves are viewed overlapping. Very folly plant. Modulus operator is 'two' which controls its structure.
Almost advanced modern plants have more complex morphology. A caulome throw out at a point of Fibonacci sequence on logarithmic spire revolved its shaft(right picture). i.e. the Golden Mean. When viewed from above, from any angle, leaves are viewed chaotic and dispersedly. That's a smart way. Its structure is the quasi-crystalline structure.
points as follows
- lighting efficiency
- stabilized structure
- strength (spreading of moment)
- effective utilization of fixed-volume
For all, plants adopted the Golden Mean have a superior structure.
Even a plant had got the complex operator in the evolution. And the Golden Mean is adopted.
The quasicrystal structure was found by Daniel Shechtman in 1982 due to AL-Mn electron diffraction method. He was awarded the Nobel Prize in Chemistry in 2011. Left picture is the Al-Pd-Mn quasicrystal atom arrangement.
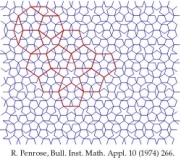
In mathematical terms, two dimentional quasicrystal structure was originated by Roger Penrose in 1974 which was so-called Penrose Tiling. And, the Fibonacci series by Leonardo Filius Bonacci in 12c ~ 13c is one dimentional aperiodical structure.
Right pictures both are the Penrose Tiling.
Comparative materials are crystal and amorphous for grasping what the quasicrystal's aspect due to compare their atom arrangement morphologies. Crystal and quasicrystal structure have long-distance order, amorphous does not.
There is different revolution symmetry between crystal and quasicrystal. Rotationally symmetrical structure of crystal are two, three, four, six (180, 120, 90, 60 degree), and quasicrystal is just five (72 degree) which structure is full of the Golden Mean.
Geometrically, three dimentional quasicrystal structure is just regular icosahedra quasicrystal, two dimentional quasicrystal are regular octagon quasicrystal and regular decagon quasicrystal, regular dodecagon quasicrystal and so on.
In an aside, A software named
Bob - Penrose Tiling Generator and Explorer for Windows by Stephen Collins is very interesting which could generate the Penrose Tiling.
I wrote following formula is complete one dimentional quasicrystal structural rhythm : f(x) = cos(2 * PI * x) + cos(2 * PI * x / r), r is the Golden Mean, r = (1 + Sqr(5)) / 2
Due to peg r at two, three..., the formula expresses one dimentional crystal structure which are same as two beats and three beats and so on as musical rhythms. For practical sound, expression is due to two diffent tones. No need to use the trig function but two dimentional gridwork which brings easy calculation.
And, due to peg r at irrational number, it could sound strange rhythm which is not adopted in music.
That's a core part function of this software.